TÓM TẮT
Tìm được 32 chủ đề phù hợp với toán 12 nguyên hàm.












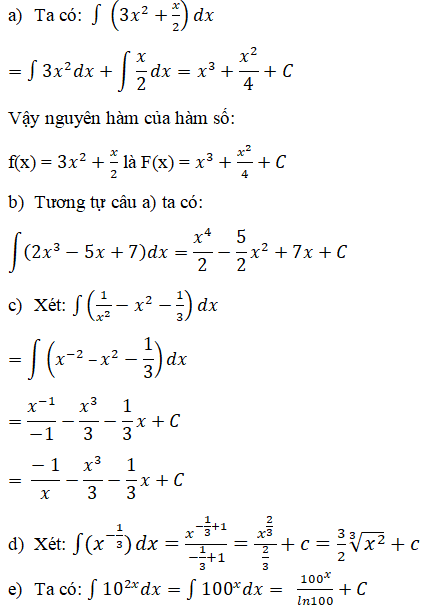


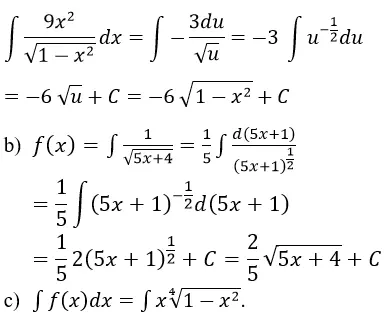









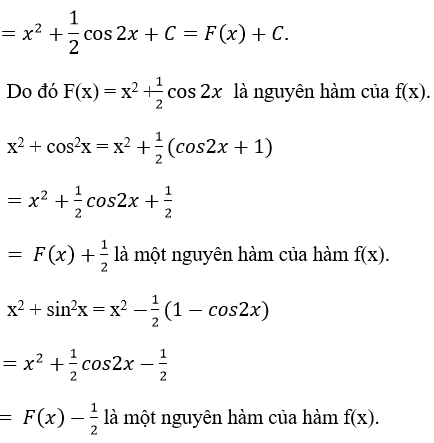









![Đại số] Nguyên Hàm, Tích Phân và những ứng dụng thực tế (kèm lời giải) - Hoctai.vn Đại Số] Nguyên Hàm, Tích Phân Và Những Ứng Dụng Thực Tế (Kèm Lời Giải) - Hoctai.Vn](https://hoctai.vn/wp-content/uploads/2019/05/toan-dai-12-1024x900.jpg)









toán 12 nguyên hàm
I. Khái niệm cơ bản về nguyên hàm trong toán 12
A. Định nghĩa nguyên hàm
Nguyên hàm của một hàm số f(x) là một hàm số F(x) mà đạo hàm của F(x) bằng f(x), tức là F'(x) = f(x). Điều này có nghĩa là F(x) là một khối lượng không đổi của f(x).
B. Các tính chất của nguyên hàm
– Nguyên hàm của một hàm số có thể không duy nhất.
– Nguyên hàm của một hàm số f(x) được kí hiệu là ∫f(x)dx.
– Nguyên hàm của hàm số f(x) + g(x) là tổng của các nguyên hàm của f(x) và g(x), nghĩa là ∫(f(x)+g(x))dx = ∫f(x)dx + ∫g(x)dx.
– Nguyên hàm của hàm số kf(x) là khối lượng của kf(x), nghĩa là ∫kf(x)dx = k∫f(x)dx.
– Nguyên hàm của hàm số f(g(x))g'(x) là ∫f(g(x))g'(x)dx.
C. Phân loại nguyên hàm
Nguyên hàm được phân loại thành hai loại chính: nguyên hàm xác định và nguyên hàm không xác định.
– Nguyên hàm xác định là nguyên hàm có giá trị tại giới hạn trên và dưới của một khoảng xác định.
– Nguyên hàm không xác định là nguyên hàm không có giới hạn trên và dưới và được biểu diễn dưới dạng tích phân chung.
II. Các phương pháp tính nguyên hàm
A. Phương pháp thế
Phương pháp thế được sử dụng để tính nguyên hàm của một hàm số bằng cách sử dụng một hàm số khác có nguyên hàm được biết đến.
Ví dụ: để tính nguyên hàm của f(x) = 2x + 3, ta sử dụng phương pháp thế với hàm số g(x) = x^2 + 3x + 5. Tính nguyên hàm của g(x), ta có G(x) = (1/3)x^3 + (3/2)x^2 + 5x + C. Tương đương với ∫f(x)dx = G(x) + C = (1/3)x^3 + (3/2)x^2 + 5x + C.
B. Phương pháp phân rã thành tổng
Phương pháp phân rã thành tổng được sử dụng để tính nguyên hàm của một hàm số được biểu diễn dưới dạng tổng các hàm số đơn giản.
Ví dụ: để tính nguyên hàm của f(x) = x^3 + 2x^2 – 5x + 3, ta có thể phân rã thành tổng các hàm số đơn giản như sau: f(x) = x^3 + 2x^2 – 5x + 3 = x^3 + x^2 + x^2 + x – 6x + 9 = x(x^2 + 1) + (x^2 – 6x + 9). Từ đó, ta tính nguyên hàm của từng hàm số trong tổng rồi cộng lại.
C. Phương pháp đổi biến số
Phương pháp đổi biến số được sử dụng để tính nguyên hàm của một hàm số bằng cách đổi biến số.
Ví dụ: để tính nguyên hàm của f(x) = 2x + 1/(x+1), ta có thể sử dụng phương pháp đổi biến số bằng cách đặt u = x + 1. Từ đó, ta có dx = du và f(x) = 2(u-1) + 1/u. Tính nguyên hàm của từng hàm số trong f(u) rồi đổi lại biến số u thành x để tính được nguyên hàm của f(x).
D. Phương pháp tích phân bởi phần tử tách biến
Phương pháp tích phân bởi phần tử tách biến được sử dụng để tính nguyên hàm của một hàm số bằng cách tích phân từng phần tử nhỏ riêng lẻ.
Ví dụ: để tính nguyên hàm của f(x) = 3x^2/(2x+1), ta sử dụng phương pháp tích phân bởi phần tử tách biến bằng cách chia tử và mẫu cho 2x+1. Từ đó, ta có f(x) = 3x^2/(2x+1) = (3/2)x – 3/(4(2x+1)) + 15/(4(2x+1)^2). Tính nguyên hàm của từng phần tử nhỏ rồi cộng lại để tính được nguyên hàm của f(x).
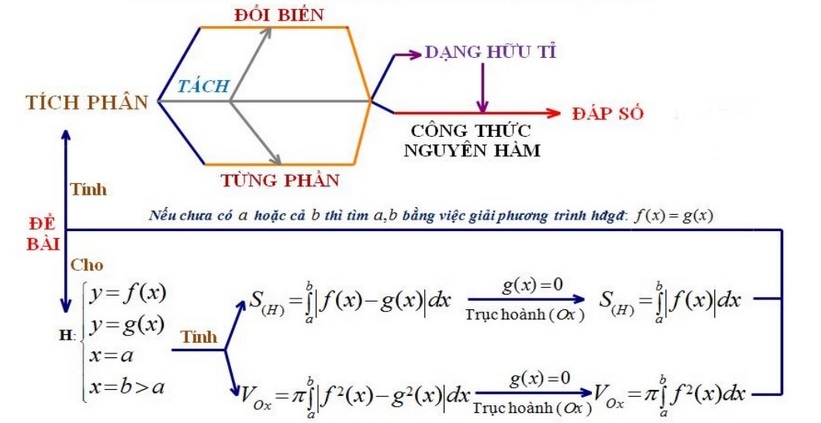
III. Ứng dụng của nguyên hàm trong tính toán
A. Tính diện tích
Nguyên hàm được sử dụng để tính diện tích của một hình thang hoặc một hình tròn.
Ví dụ: để tính diện tích của một hình thang có đáy là 4, đỉnh là 3, và chiều cao là 2, ta có hàm số f(x) = 2x + 2. Tính nguyên hàm của f(x) từ 3 đến 7 để tính được diện tích.
B. Tính thể tích
Nguyên hàm được sử dụng để tính thể tích của một hình trụ hoặc một hình chóp.
Ví dụ: để tính thể tích của một hình trụ có bán kính là 4 và chiều cao là 6, ta có hàm số f(x) = 16π – πx^2. Tính nguyên hàm của f(x) từ 0 đến 6 để tính được thể tích.
C. Tính lượng giác
Nguyên hàm được sử dụng để tính lượng giác của một hình tròn.
Ví dụ: để tính lượng giác của một đoạn cung có cung bằng 60 độ và bán kính là 5, ta có hàm số f(x) = 5cos(x). Tính nguyên hàm của f(x) từ -π/6 đến π/6 để tính được lượng giác.
D. Tính tốc độ và gia tốc trong bài toán vật lý
Nguyên hàm được sử dụng trong bài toán vật lý để tính tốc độ và gia tốc của một chuyển động.
Ví dụ: để tính tốc độ của một đối tượng di chuyển theo đường thẳng với tốc độ ban đầu là 10m/s và gia tốc là -2m/s^2 trong 10 giây, ta có hàm số f(x) = -2x + 10. Tính nguyên hàm của f(x) từ 0 đến 10 để tính được tốc độ của đối tượng sau 10 giây.
FAQs
Q: Có bao nhiêu loại nguyên hàm?
A: Nguyên hàm được phân loại thành hai loại chính: nguyên hàm xác định và nguyên hàm không xác định.
Q: Có bao nhiêu phương pháp tính nguyên hàm?
A: Có bốn phương pháp chính để tính nguyên hàm là phương pháp thế, phương pháp phân rã thành tổng, phương pháp đổi biến số, và phương pháp tích phân bởi phần tử tách biến.
Q: Nguyên hàm có ứng dụng gì trong tính toán?
A: Nguyên hàm có ứng dụng trong tính toán diện tích, thể tích, lượng giác, và trong bài toán vật lý để tính tốc độ và gia tốc của một chuyển động.
Từ khoá người dùng tìm kiếm: toán 12 nguyên hàm Toán 12 nguyên hàm lý thuyết, Bài tập nguyên hàm SGK, Toán 12 nguyên hàm trang 100, Nguyên hàm 12 trang 101, Toán 12 nguyên hàm bài 4, Giải bài tập nguyên hàm, Giải nguyên hàm online, Toán 12 Bài 1 : nguyên hàm
Tag: Collection 62 – toán 12 nguyên hàm
Nguyên Hàm Cơ Bản Và Mở Rộng – Toán 12 | Thầy Nguyễn Công Chính
Xem thêm tại đây: buoitutrung.com
Link bài viết: toán 12 nguyên hàm.
Xem thêm thông tin về chủ đề toán 12 nguyên hàm.
- Giải Toán 12 Bài 1 : Nguyên hàm – VietJack.com
- Toán 12 Nguyên Hàm – Lý Thuyết, Công Thức Và Bài Tập
- Nguyên hàm – Toán 12 – Loigiaihay.com
- Đáp số và lời giải toán 12 bài nguyên hàm – Kiến Guru
- Toán 12: Nguyên Hàm – Giải bài tập SGK (Hay nhất)
- Giải bài tập trang 100, 101 SGK Giải Tích 12 – Nguyên hàm
- Giải bài tập SGK Toán 12 Bài 1: Nguyên hàm
- Toán 12 Nguyên Hàm: Lý Thuyết Và Cách Giải Bài Tập
Categories: https://baannapleangthai.com/img/

