Ngoài ra, bài tập này còn đòi hỏi học sinh phải biết áp dụng các kiến thức về hình học để giải quyết các vấn đề thực tế trong cuộc sống. Việc làm chính xác và một cách nhanh chóng các phép tính trong bài tập này sẽ giúp học sinh nâng cao kỹ năng giải toán và đạt kết quả tốt trong kì thi học kỳ hay kỳ thi tốt nghiệp.
Để đạt được thành công trong bài tập này, học sinh cần tập trung học tập và rèn luyện kỹ năng từ những kiến thức cơ bản đến những kỹ năng phân tích và giải quyết vấn đề. Ngoài ra, học sinh cũng cần nâng cao hiểu biết về các vấn đề liên quan đến hình học trong cuộc sống hàng ngày, giúp họ áp dụng kiến thức một cách linh hoạt và hiệu quả.
Toán hình 11 bài 3 là một bài tập đòi hỏi sự chăm chỉ, cẩn trọng và kiên trì của học sinh trong quá trình học tập. Với sự nỗ lực và cố gắng không ngừng, học sinh có thể thanh công trong việc giải quyết các bài tập hình học và đạt được kết quả tốt trong kì thi.
TÓM TẮT
Tìm được 30 bài viết liên quan đến chủ đề toán hình 11 bài 3.









![TÀI LIỆU 11] - TÀI LIỆU TỰ HỌC - CHƯƠNG 3. QUAN HỆ VUÔNG GÓC Tài Liệu 11] - Tài Liệu Tự Học - Chương 3. Quan Hệ Vuông Góc](https://1.bp.blogspot.com/-rBC-aXlq5G8/YR3f3qXJ5FI/AAAAAAAAEbU/kjusXrPHOR0nszYsVJM_Vrc8fGlhjUDtgCLcBGAsYHQ/w0/1H3.png)










.png)

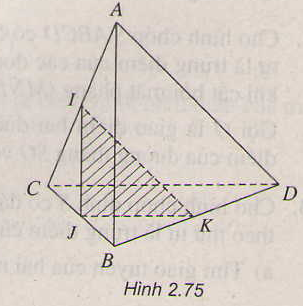
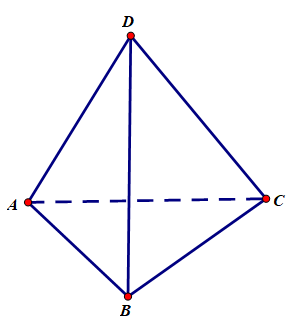



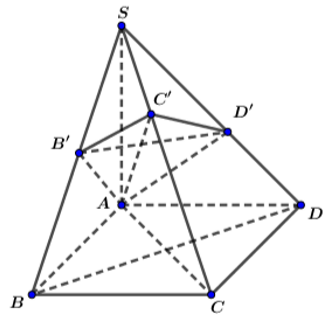



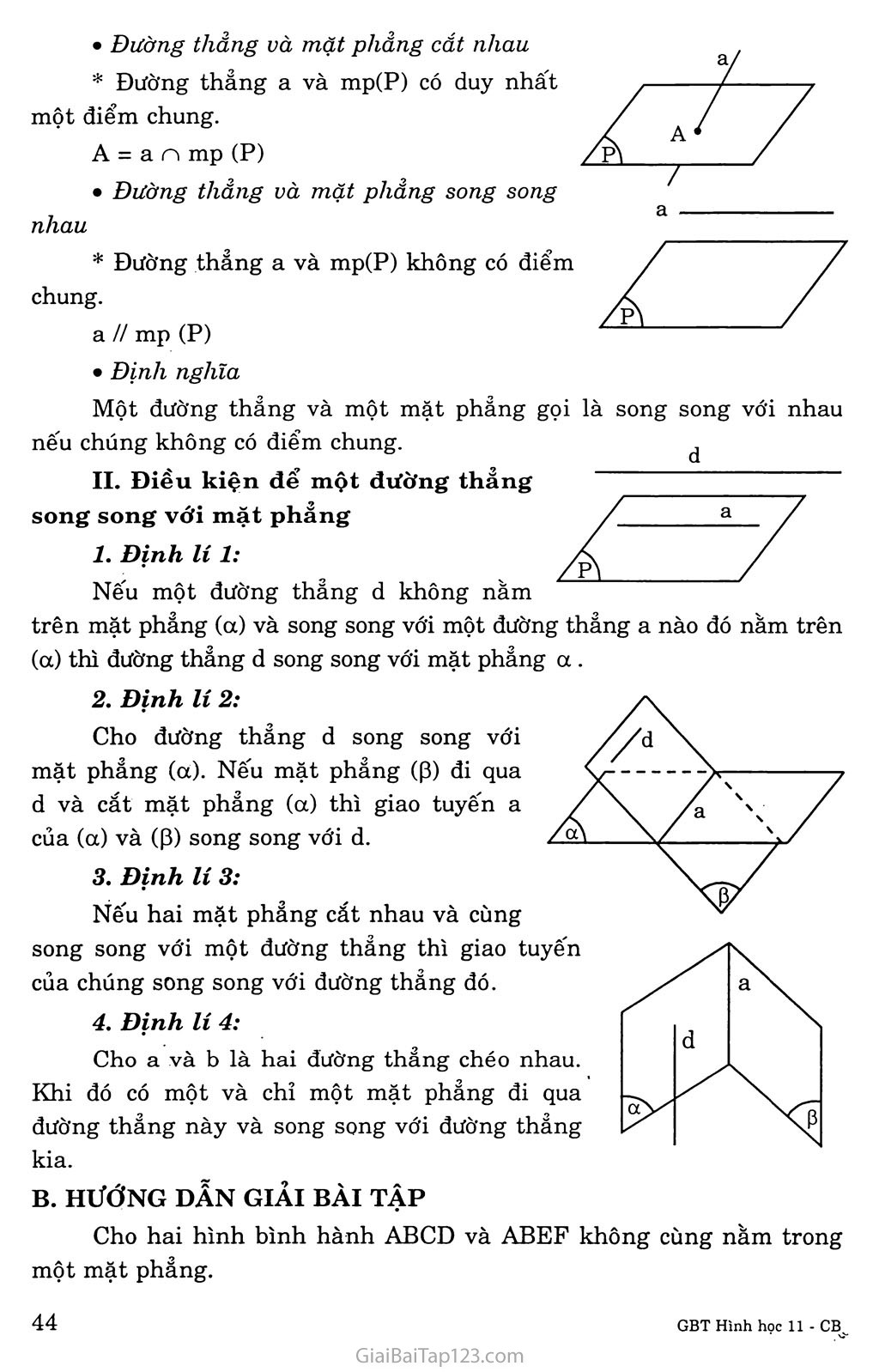



toán hình 11 bài 3
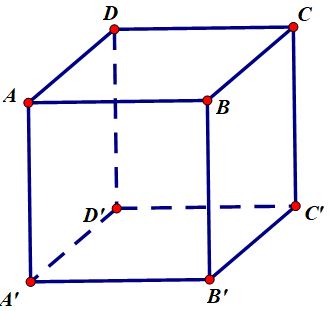
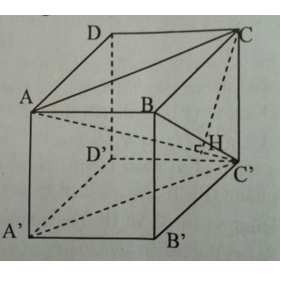
Hình hộp chữ nhật là một trong những hình phổ biến nhất trong toán hình. Nó được định nghĩa là một hình có 6 mặt, trong đó 4 mặt hình chữ nhật song song và cặp đối diện của nó bằng nhau. Để tính diện tích hình hộp chữ nhật, ta có công thức:
Diện tích hình hộp chữ nhật = 2(ab + ac + bc)
Trong đó, a, b và c lần lượt là chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật. Để tính thể tích hình hộp chữ nhật, ta sử dụng công thức sau:
Thể tích hình hộp chữ nhật = abc
Khối chóp cũng được sử dụng rất nhiều trong toán hình 11 bài 3. Định nghĩa của khối chóp là một hình có đáy là một đa giác bất kỳ và các cạnh của đáy đều vuông góc với đáy. Để tính diện tích của khối chóp, ta có công thức là:
Diện tích khối chóp = diện tích đáy + diện tích các mặt bên
Trong đó, diện tích các mặt bên được tính bằng cách lấy nửa chu vi đáy nhân với độ dài cạnh bên. Để tính thể tích của khối chóp, ta sử dụng công thức:
Thể tích khối chóp = 1/3 diện tích đáy x chiều cao
Ví dụ về ứng dụng của hình hộp chữ nhật và khối chóp là trong công nghiệp và kiến trúc. Chúng được sử dụng để tính toán diện tích và thể tích của các đồ vật và công trình, giúp cho quá trình thiết kế, sản xuất và vận chuyển trở nên chính xác hơn.
Hình cầu là một hình rất đặc biệt và quan trọng trong toán hình 11 bài 3. Hình cầu được định nghĩa là một hình tròn được quay xoay 360 độ xung quanh trục của nó. Để tính diện tích hình cầu, ta sử dụng công thức sau:
Diện tích hình cầu = 4πr2
Trong đó, r là bán kính của hình cầu. Để tính thể tích hình cầu, ta có công thức sau:
Thể tích hình cầu = 4/3πr3
Ví dụ về ứng dụng của hình cầu là trong sản xuất các viên bi, hình cầu được sử dụng để tính toán diện tích và thể tích của các sản phẩm này.
Hình trụ cũng là một hình quan trọng trong toán hình 11 bài 3. Định nghĩa của hình trụ là một hình có đáy là một hình tròn và các mặt bên là các hình chữ nhật. Để tính diện tích hình trụ, ta sử dụng công thức sau:
Diện tích hình trụ = 2πr2 + 2πrh
Trong đó, r là bán kính đáy của hình trụ và h là chiều cao của hình trụ. Để tính thể tích của hình trụ, ta có công thức:
Thể tích hình trụ = πr2h
Ví dụ về ứng dụng của hình trụ là trong sản xuất các lon đồ uống, hình trụ được sử dụng để tính toán diện tích và thể tích của các sản phẩm này.
Hình nón cũng là một hình phổ biến và quan trọng trong toán hình 11 bài 3. Định nghĩa của hình nón là một hình có đáy là một hình tròn và các mặt bên là các tam giác đều. Để tính diện tích hình nón, ta sử dụng công thức sau:
Diện tích hình nón = πr2 + πrl
Trong đó, r là bán kính đáy của hình nón và l là độ dài đường sinh của hình nón. Để tính thể tích của hình nón, ta có công thức sau:
Thể tích hình nón = 1/3πr2h
Ví dụ về ứng dụng của hình nón là trong sản xuất các đồ chơi trẻ em như xe lửa, hình nón được sử dụng để tính toán diện tích và thể tích của các sản phẩm này.
FAQs
1. Tại sao hình hộp chữ nhật và khối chóp được sử dụng phổ biến trong giáo dục và ứng dụng?
– Vì hình hộp chữ nhật và khối chóp là các hình đơn giản và phổ biến trong cuộc sống hằng ngày, có nhiều ứng dụng trong đời sống và công nghiệp.
2. Tại sao hình cầu, hình trụ và hình nón được coi là các hình quan trọng?
– Vì chúng là những hình đặc biệt và có nhiều ứng dụng trong các lĩnh vực như kỹ thuật, kiến trúc, sản xuất,…
3. Tại sao lại có quy tắc đặt tên các hình học như vậy?
– Cách đặt tên các hình học được xây dựng dựa trên các chức năng và tính chất của các hình.
4. Những công thức nào quan trọng nhất khi tính diện tích và thể tích của các hình học trong toán hình 11 bài 3?
– Các công thức quan trọng nhất là diện tích hình hộp chữ nhật, diện tích khối chóp, diện tích hình trụ, diện tích hình nón và thể tích của các hình này.
5. Tại sao phải học toán hình 11 bài 3?
– Học toán hình 11 bài 3 giúp các bạn có thể hiểu về các khái niệm căn bản trong hình học và áp dụng chúng vào thực tế. Nó cũng giúp các bạn hoàn thiện kỹ năng tính toán và tư duy logic của mình.
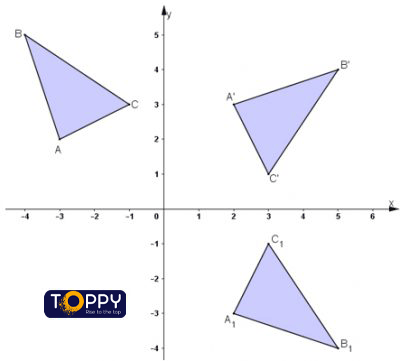
Từ khoá người dùng tìm kiếm: toán hình 11 bài 3 toán hình 11 bài 3: đường thẳng vuông góc, toán hình 11 bài 3: đường thẳng và mặt phẳng song song, Bài 3 Toán hình 11 lý thuyết, Bài 3 Toán hình 11 trang 104, toán hình 11 bài 3: phép đối xứng trục, Toán Hình 11 Bài 3 Chương 3, Toán Hình 11 Bài 3 chương 2, Toán hình 11 Bài 3: đường thẳng vuông góc với mặt phẳng
Tag: Collection 84 – toán hình 11 bài 3
Toán học lớp 11 – Hình học – Chương 3 – Bài 3 – Đường thẳng vuông góc với mặt phẳng – Tiết 1
Xem thêm tại đây: buoitutrung.com
Link bài viết: toán hình 11 bài 3.
Xem thêm thông tin về chủ đề toán hình 11 bài 3.
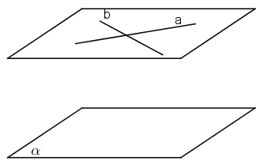
- Hình học 11 Bài 3: Đường thẳng và mặt phẳng song song
- Sách Giải Bài Tập Toán Lớp 11 Bài 3: Phép Đối Xứng Trục
- Soạn hình học 11 bài 3: Phép đối xứng trục – hocthoi
- Bài 3 trang 7 SGK Hình học 11 | Giải bài tập Toán 11 – Toploigiai
- Giải Toán hình 11 Bài 3: Đường thẳng vuông góc với mặt phẳng
Categories: https://baannapleangthai.com/img/

