Để tính toán tam giác, chúng ta cần biết các thông số cơ bản như độ dài các cạnh, độ dài các đường cao và độ dài đường trung tuyến. Ngoài ra, các công thức tính diện tích, chu vi và những đặc tính khác cũng rất quan trọng.
Tính hình tam giác cũng liên quan đến các định lí và khái niệm quan trọng như định lí Pythagoras, định lí Cosin và định lí Sin. Các công thức và định lí này không chỉ giúp chúng ta tính toán tam giác một cách chính xác mà còn cung cấp cho chúng ta một cách nhìn sâu sắc vào tính chất và cấu trúc của tam giác.
Trên thực tế, tính hình tam giác không chỉ sử dụng trong toán học mà còn trong các ngành công nghiệp và kỹ thuật. Ví dụ, trong kiến trúc, tính toán hình dạng tam giác và diện tích giúp xác định lượng vật liệu cần thiết để xây dựng công trình. Trong công nghệ đường ống, tính toán tam giác giúp xác định kích thước và định vị các khoảng cách giữa các đường ống.
Tóm lại, tính hình tam giác là một chủ đề quan trọng trong toán học và hình học. Tính chất của tam giác đóng vai trò quan trọng trong nhiều lĩnh vực và là một phần không thể thiếu của đời sống hàng ngày.
TÓM TẮT
Tìm được 37 chủ đề phù hợp với tính hình tam giác.












![Diện Tích Hình Tam Giác ] Vuông, Cân, Thường, Đều, Công Thức, Cách tính Diện Tích Hình Tam Giác ] Vuông, Cân, Thường, Đều, Công Thức, Cách Tính](https://apecceosummit2017.com.vn/wp-content/uploads/2019/10/cong-thuc-tinh-dien-tich-tam-giac-vuong.png)


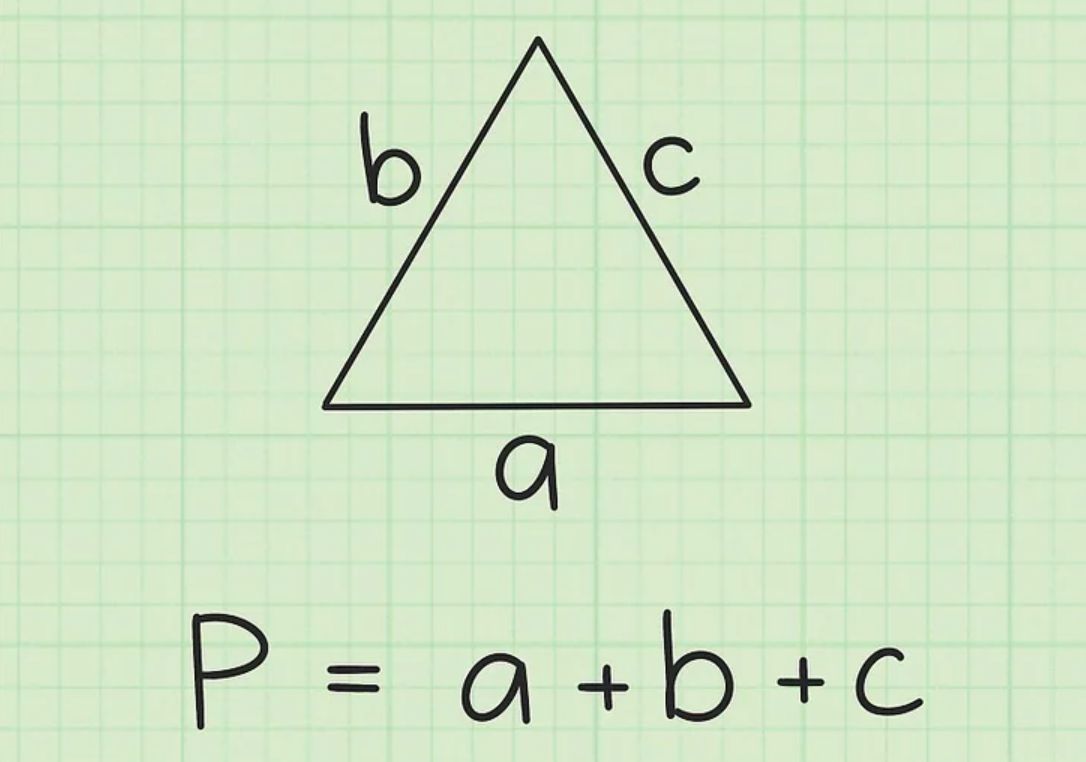






tính hình tam giác
Khái niệm tam giác và các thành phần của tam giác
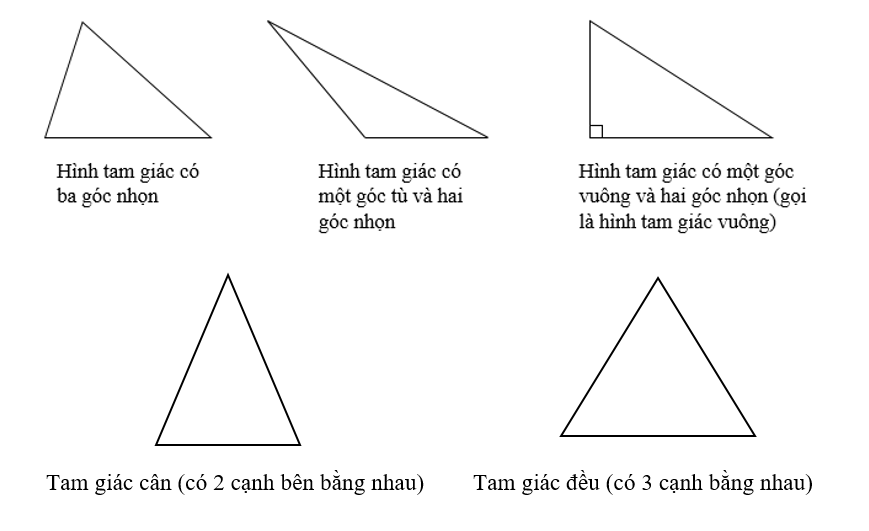
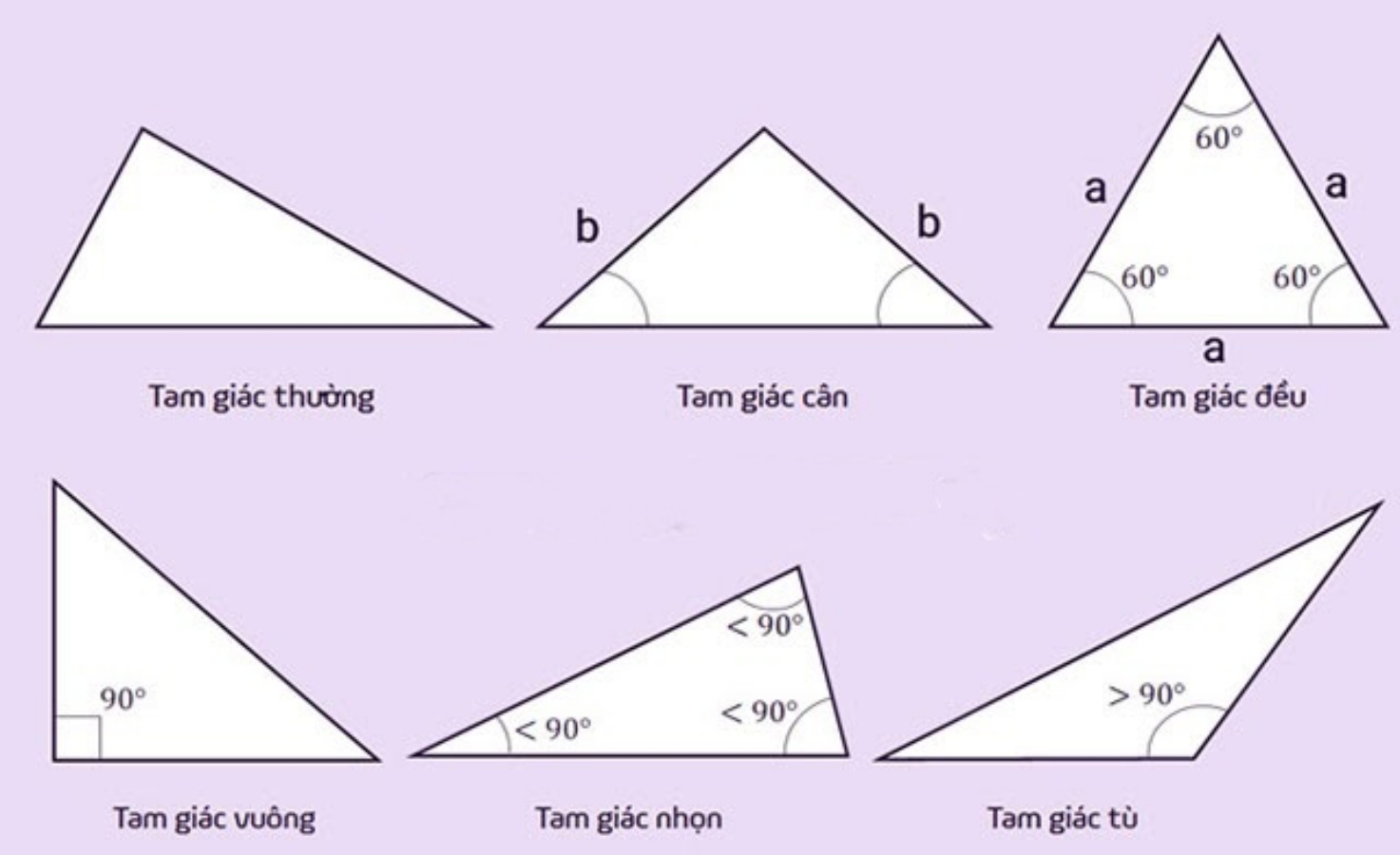
Tam giác là một hình học có ba đỉnh và ba cạnh. Các điểm giao nhau của các cạnh được gọi là đỉnh của tam giác và các cạnh được gọi là cạnh của tam giác. Tam giác có thể được phân loại theo các đặc điểm của nó, như độ dài các cạnh và các góc của nó.
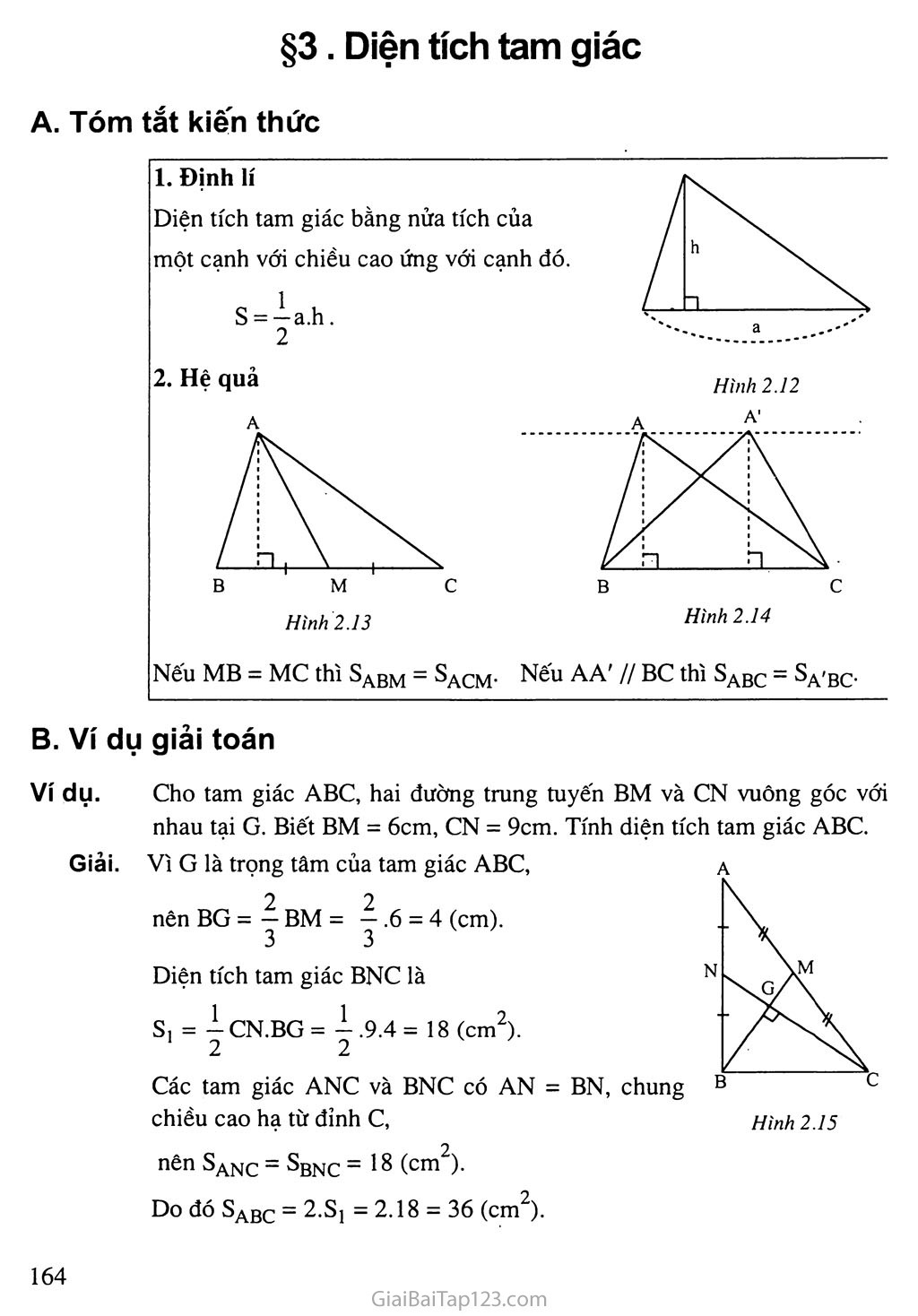
Công thức tính diện tích tam giác và một số bài tập ví dụ
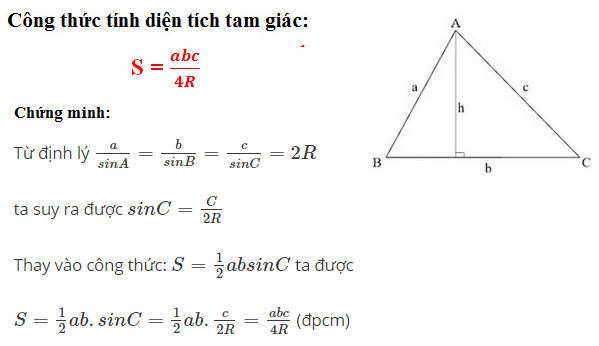
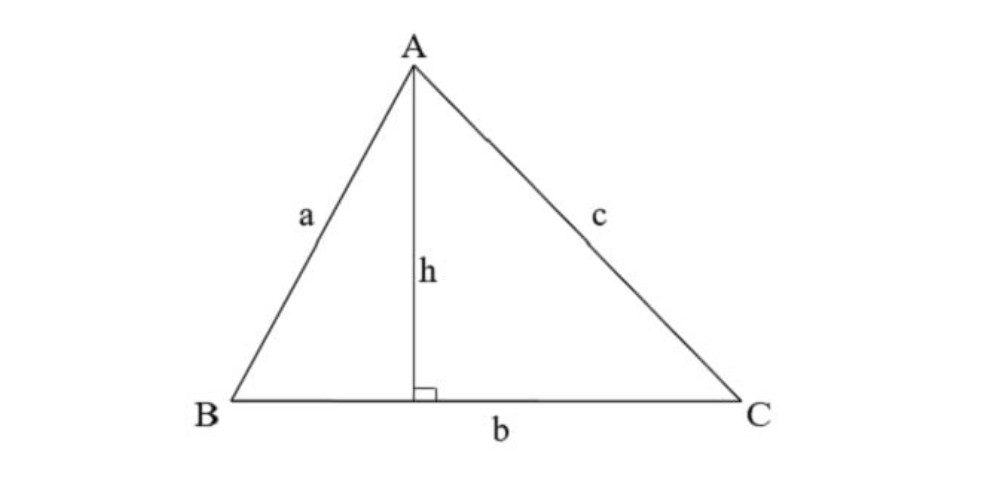
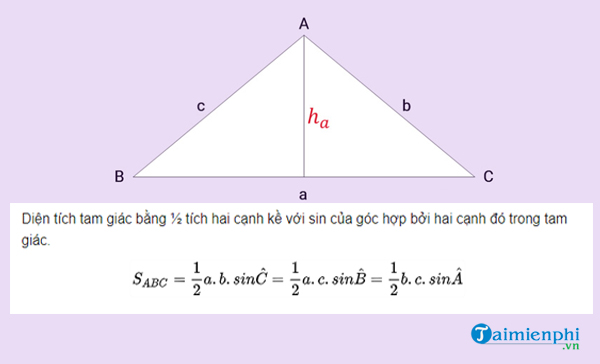
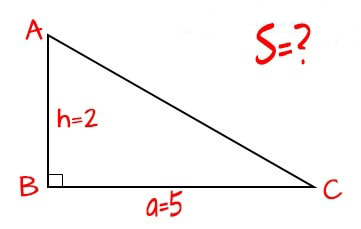
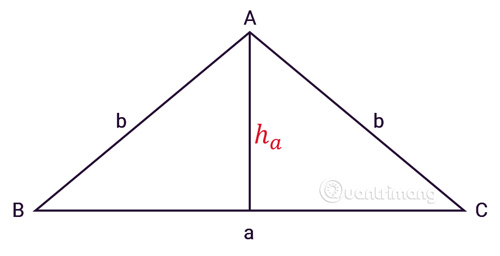
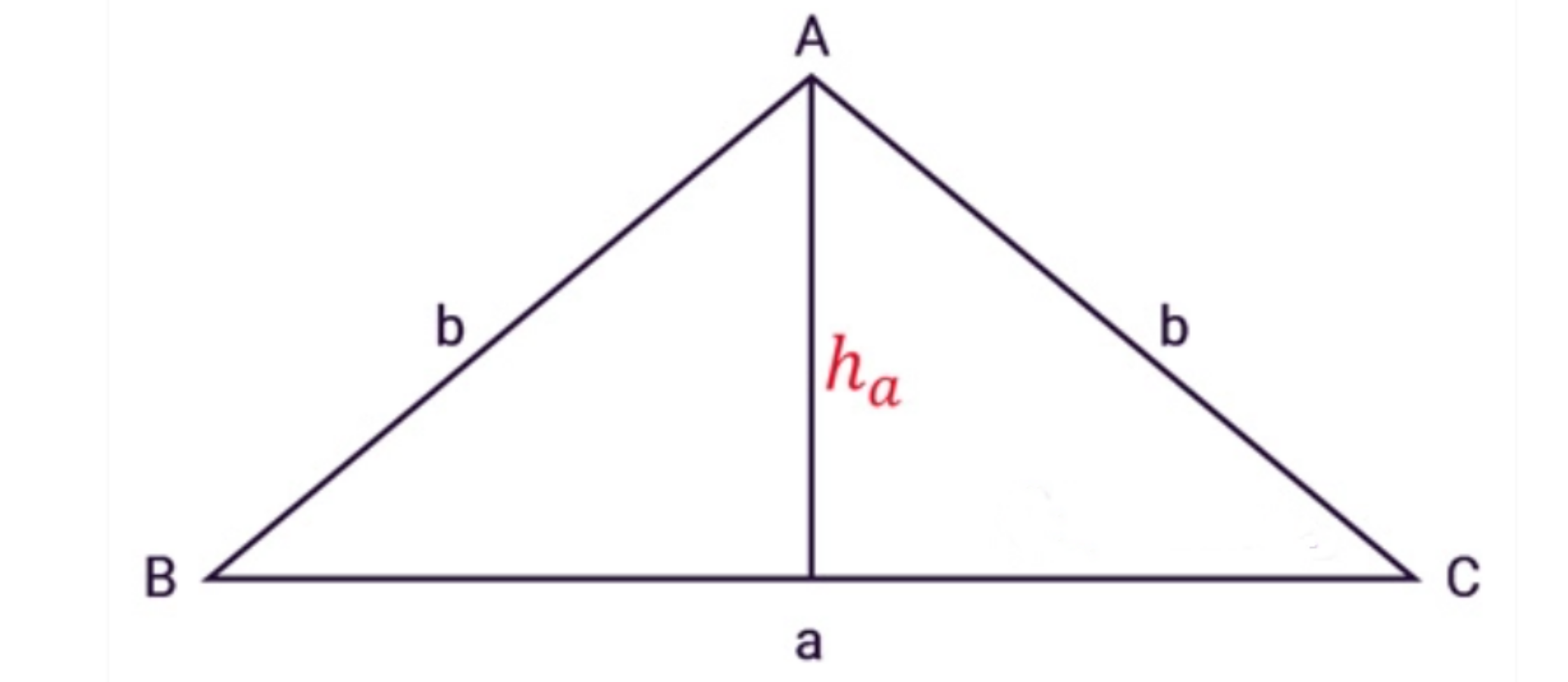
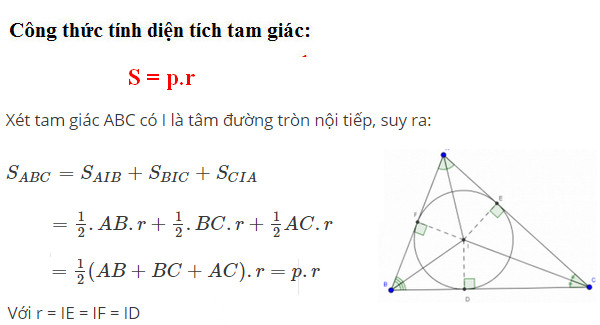
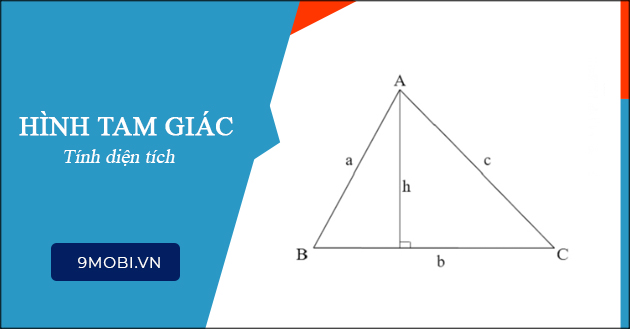
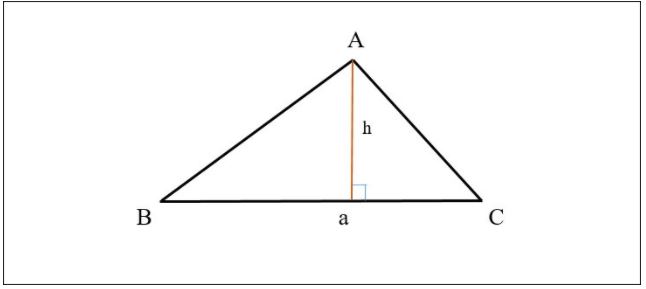
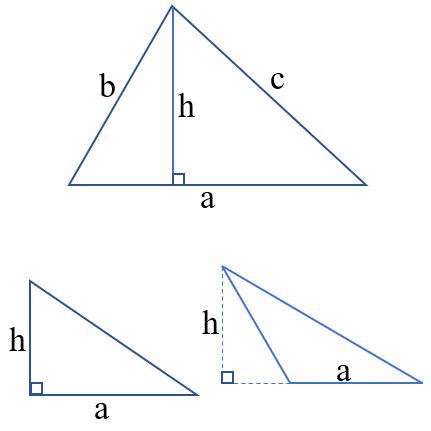
Diện tích tam giác được tính bằng công thức sau:
Diện tích = 1/2 x cạnh đáy x chiều cao.
Ví dụ, hãy tính diện tích của một tam giác có cạnh đáy là 6 và chiều cao là 4.
Giải:
Diện tích = 1/2 x 6 x 4 = 12.
Một ví dụ khác, hãy tính diện tích của một tam giác có độ dài các cạnh là 5, 6 và 7.
Để tính diện tích của tam giác này, ta có thể sử dụng công thức Heron:
Diện tích = căn bậc hai của p x (p – a) x (p – b) x (p – c),
trong đó p được tính bằng nửa chu vi của tam giác:
p = (a + b + c) / 2.
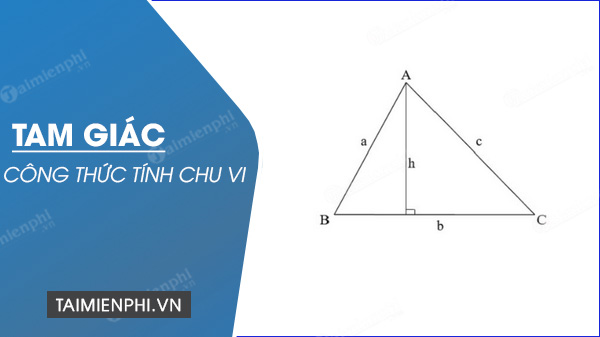
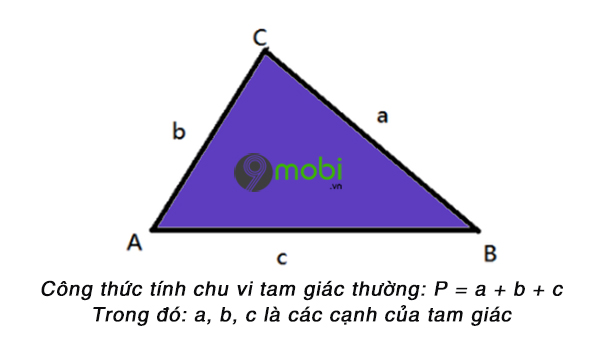
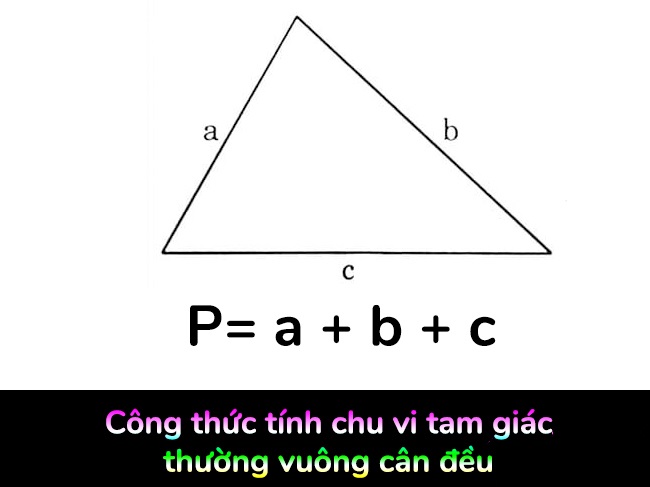
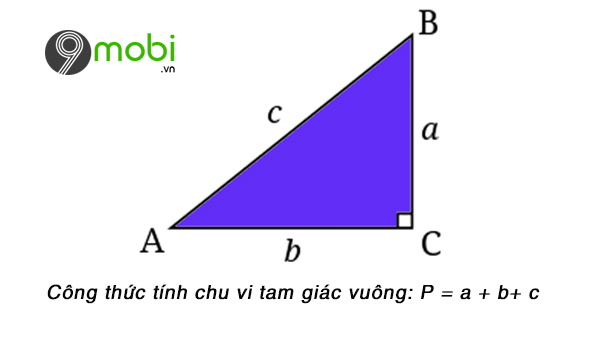
Chu vi của tam giác có thể được tính bằng công thức đơn giản sau:
Chu vi = a + b + c.
Các định lí tam giác về góc, độ dài cạnh, đường trung trực và đường cao
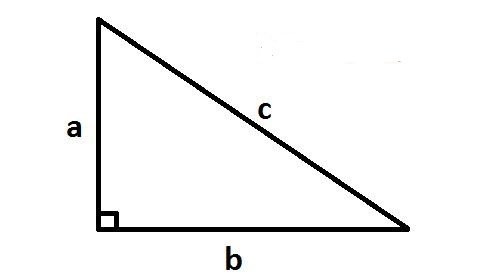
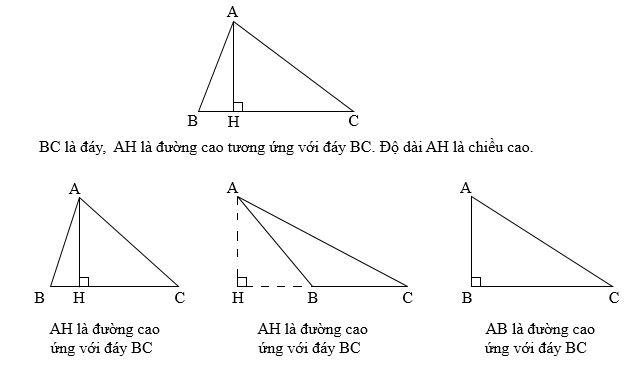
Các định lí tam giác giúp chúng ta hiểu thêm về các đặc điểm thú vị của tam giác. Ví dụ, định lí Pitago cho biết rằng trong tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông. Định lí đường trung trực cho biết rằng mỗi cạnh của tam giác có một đường trung trực tương ứng, và đường trung trực này giao nhau ở một điểm gọi là trung điểm của cạnh. Định lí đường cao cho biết rằng mỗi tam giác đều có một đường cao tương ứng, và đường cao này là đoạn thẳng nối đỉnh của tam giác với cạnh đối diện và vuông góc với cạnh đó.
Ứng dụng của tỷ lệ tiến độ và định lí Pitago trong tính toán tam giác
Trong nhiều trường hợp, chúng ta có thể sử dụng các định lí tam giác và các tỷ lệ tiến độ để giúp tính toán diện tích và chu vi của tam giác. Ví dụ, nếu ta có hai tam giác có các cạnh tương đồng, ta có thể sử dụng tỷ lệ tiến độ để tìm ra diện tích của chúng. Ngoài ra, định lí Pitago có thể được sử dụng để tính toán các độ dài cạnh của tam giác vuông.
Sử dụng tính hình tam giác trong các bài toán giải trí và thực tế
Tính hình tam giác có rất nhiều ứng dụng trong giải trí và thực tế. Chẳng hạn, trong các trò chơi sudoku, các ô vuông được phân chia thành nhiều tam giác vuông nhỏ để giúp người chơi giải quyết bài toán. Trong kiến trúc, các tam giác được sử dụng để thiết kế các kết cấu chắc chắn và đẹp mắt.
Các ứng dụng của hình học tam giác trong khoa học và công nghệ
Thêm vào đó, tính hình tam giác cũng có các ứng dụng đáng kể trong khoa học và công nghệ. Trong khoa học máy tính, tính toán tam giác được sử dụng để thiết kế các giải thuật và phân tích dữ liệu. Các kỹ sư cơ khí và xây dựng cũng sử dụng nhiều kỹ thuật hình học tam giác trong thiết kế thiết bị và kết cấu.
FAQs
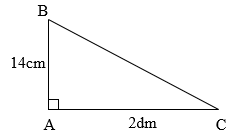
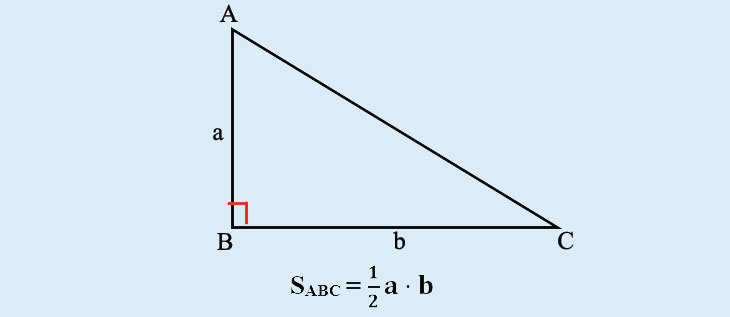
1. Tính diện tích tam giác vuông là gì?
Diện tích tam giác vuông được tính bằng công thức sau: Diện tích = 1/2 x độ dài cạnh góc vuông 1 x độ dài cạnh góc vuông 2.
2. Cách tính diện tích hình tam giác lớp 5?
Để tính diện tích tam giác, chúng ta sử dụng công thức Diện tích = 1/2 x cạnh đáy x chiều cao.
3. Chu vi hình tam giác là gì?
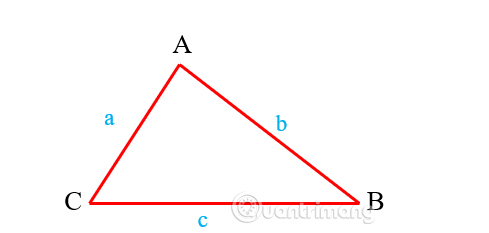
Chu vi hình tam giác là tổng độ dài của các cạnh của tam giác. Công thức tính chu vi là Chu vi = a + b + c.
4. Tính diện tích tam giác vuông, cân là gì?
Diện tích tam giác vuông, cân được tính bằng công thức Diện tích = cạnh đáy x chiều cao / 2.
5. Công thức tính diện tích tam giác là gì?
Công thức tính diện tích tam giác là Diện tích = 1/2 x cạnh đáy x chiều cao.
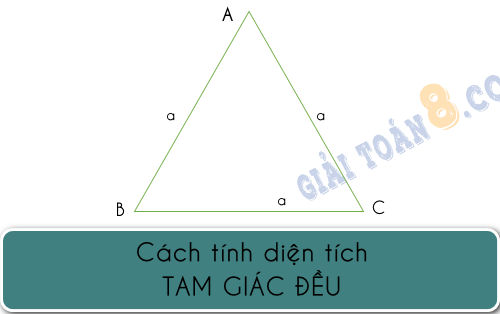
6. Cách tính diện tích tam giác đều là gì?
Diện tích tam giác đều được tính bằng công thức Diện tích = căn bậc hai của 3 x độ dài cạnh một cạnh / 2.
7. Công thức tính diện tích tam giác vuông lớp 5 là gì?
Công thức tính diện tích tam giác vuông lớp 5 là Diện tích = 1/2 x độ dài cạnh góc vuông 1 x độ dài cạnh góc vuông 2.
Từ khoá người dùng tìm kiếm: tính hình tam giác Tính diện tích tam giác vuông, Tính diện tích hình tam giác, Cách tính diện tích hình tam giác lớp 5, Chu vi hình tam giác, tính diện tích tam giác vuông, cân, Diện tích tam giác đều, Các công thức tính diện tích tam giác, Công thức tính diện tích tam giác vuông lớp 5
Tag: Album 67 – tính hình tam giác
Diện tích hình tam giác – Toán lớp 5 – Cô Phan Giang (DỄ HIỂU NHẤT)
Xem thêm tại đây: buoitutrung.com
Link bài viết: tính hình tam giác.
Xem thêm thông tin về chủ đề tính hình tam giác.
- Công thức tính diện tích hình tam giác – LabVIETCHEM
- Công thức tính diện tích hình tam giác và bí quyết học cực dễ
- Công thức tính diện tích tam giác: vuông, thường, cân, đều
- Công thức và cách tính chu vi, diện tích của hình tam giác
- Công thức tính diện tích tam giác (cập nhất mới nhất 2023)
- Tam giác? Công thức tính diện tích tam giác thường, vuông …
- Công Thức Tính Diện Tích Tam Giác Vuông, Đều, Tam Giác Cân
- Công thức Diện tích hình Tam Giác & Cách tính đơn giản 2023
- Lý thuyết tam giác. diện tích hình tam giác toán 5
Categories: buoitutrung.com/img
