Để học tốt bài này, học sinh cần phải có kiến thức cơ bản về toán hình và tính toán đại số. Ngoài ra, việc ôn tập các chủ đề trước đó như hình học phẳng cũng rất quan trọng để giúp học sinh nắm vững các khái niệm và áp dụng chúng vào thực tế.
Với những kiến thức và kỹ năng học được từ bài học này, học sinh sẽ có thể áp dụng vào các bài toán thực tế như tính toán thể tích của các hình khối, tính diện tích bề mặt của các đồ vật… và đặc biệt là ứng dụng trong các ngành công nghiệp, xây dựng, hàng hải, địa chất học…
Tóm lại, bài học Toán hình 11 bài 6 là một chủ đề rất thú vị và có tính ứng dụng cao trong thực tế. Đó là nguồn động lực để chúng ta học tập, nắm vững kiến thức và phát triển kỹ năng để sử dụng chúng trong cuộc sống hàng ngày.
TÓM TẮT
Có 20 bài viết liên quan đến toán hình 11 bài 6.



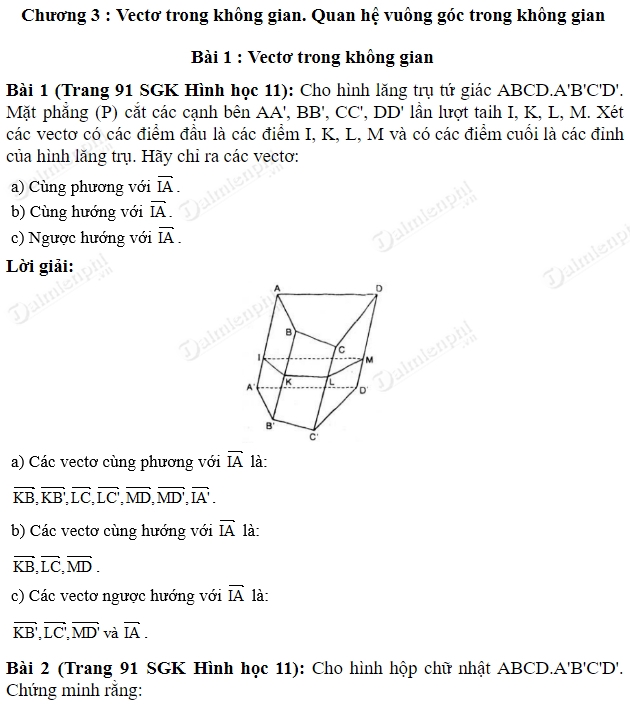








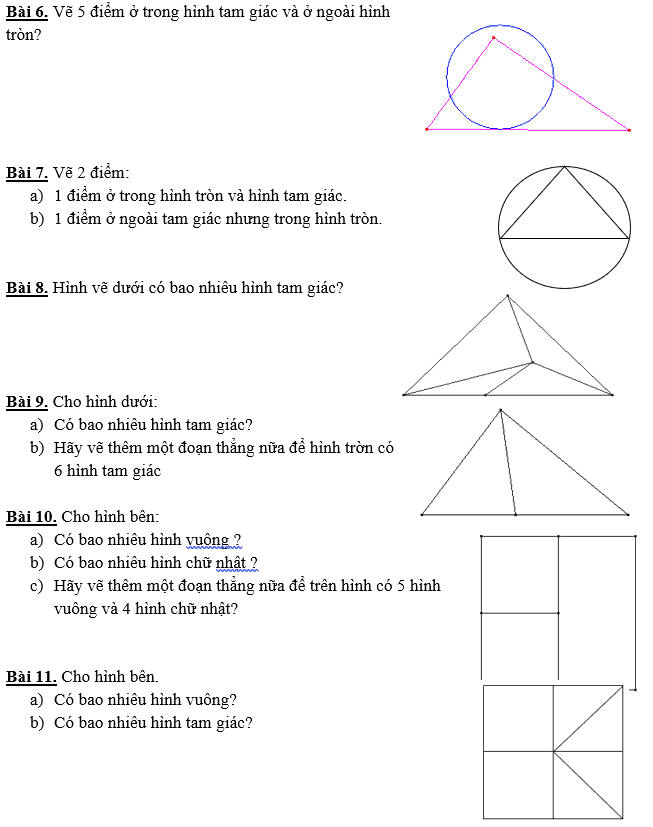

.png)







toán hình 11 bài 6
# Các khái niệm chính trong bài toán hình 11 bài 6
– Điểm, đoạn, đường thẳng: Điểm là một đối tượng không có kích thước và không có hướng. Đoạn là một phần của đường thẳng giới hạn bởi hai điểm đầu mút. Đường thẳng là một tập hợp các điểm xếp liền nhau vô hạn cùng một hướng.
– Song song, vuông góc: Hai đường thẳng được gọi là song song nếu chúng không cắt nhau. Hai đường thẳng vuông góc khi giao nhau tạo thành một góc 90 độ.
– Tâm, bán kính, đường kính: Tâm của một đường tròn là điểm nằm chính giữa đường tròn. Bán kính là khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn. Đường kính là khoảng cách qua tâm của hai điểm trên đường tròn.
– Đường tròn ngoại tiếp, nội tiếp: Đường tròn ngoại tiếp nếu nó tiếp xúc với các cạnh của một đa giác và các tia này cùng gặp tại một điểm trên đường tròn ngoại tiếp. Đường tròn nội tiếp là đường tròn tiếp xúc với các cạnh của đa giác và được đặt bên trong đa giác.
– Hình tròn đối xứng: Hình tròn đối xứng khi bất kỳ hai điểm nào cách tâm cùng một khoảng cách đều ở trên đường tròn.
# Các công thức tính trong bài toán hình 11 bài 6
– Chu vi và diện tích đa diện: Chu vi của đa diện là tổng chiều dài của các cạnh. Diện tích đa diện được tính bằng cách chia đa giác thành các tam giác và tính diện tích của các tam giác đó.
– Chu vi và diện tích hình tròn: Chu vi của hình tròn là 2πr, diện tích hình tròn là πr^2. Trong đó, r là bán kính của hình tròn.
– Thể tích hình cầu và hình trụ: Thể tích hình cầu được tính bằng công thức 4/3πr^3. Thể tích hình trụ là πr^2h, trong đó, r là bán kính đáy, h là chiều cao của hình trụ.
– Các tính chất của hình cầu và hình trụ: Hình cầu có tính chất đối xứng và có diện tích bề mặt là 4πr^2. Hình trụ có tính chất đối xứng qua mặt căn cứ và có diện tích bề mặt là 2πrh+2πr^2.
– Bài tập ví dụ về tính toán: Ví dụ như tính diện tích và chu vi của hình chữ nhật, tính thể tích của một hình hộp chữ nhật, tính diện tích mặt cầu và chu vi đường tròn ngoại tiếp của tam giác.
# Các phương pháp giải quyết bài toán hình 11 bài 6
– Vẽ hình, xác định các thông số: Đầu tiên, ta cần vẽ hình và xác định các thông số liên quan đến hình, bao gồm độ dài, bán kính, diện tích, thể tích, vị trí, các góc, và các đường thẳng.
– Áp dụng công thức tính: Sau đó, ta áp dụng các công thức tính chu vi, diện tích, thể tích của hình học để tính toán.
– Giải hệ phương trình: Trong một số trường hợp, ta có thể phải giải hệ phương trình để tìm các giá trị của các đại lượng trong bài toán.
– Sử dụng các định lí liên quan: Nếu bài toán có các định lí liên quan, chúng ta có thể áp dụng các định lí đó để giải quyết bài toán.
– Lập phương trình và giải quyết: Có thể xây dựng phương trình tương ứng với hình học trong bài toán, và giải quyết để tìm các giá trị cần thiết.
# Bài tập phân tích và giải quyết bài toán hình 11 bài 6
Để giải quyết bài toán hình 11 bài 6, chúng ta cần thực hành nhiều bài tập. Sau đây là các bước phân tích và giải quyết bài tập mẫu.
– Tính toán chuẩn bị cho bài tập: Đọc kỹ đề bài, xác định loại hình geometry và tìm hiểu các công thức, khái niệm liên quan.
– Đọc và nhận biết yêu cầu của bài: Để thực hiện bài tập, cần phải hiểu chính xác yêu cầu của bài toán và các thông tin sẵn có.
– Áp dụng kiến thức đã học để giải quyết bài tập: Áp dụng các công thức và phương pháp giải quyết để tìm ra đáp án chính xác.
– Kiểm tra và sửa chữa lỗi sai: Kiểm tra lại kết quả tính toán và sửa chữa các lỗi sai có thể gặp phải.
– Hoàn thành bài tập và đánh giá kết quả: Nhận xét kết quả đã tìm được đúng hay không và đánh giá khả năng giải quyết các bài tập hình học tương tự.
# Ứng dụng của toán hình 11 bài 6
Toán học là một lĩnh vực rất quan trọng không chỉ trong giáo dục mà còn trong cuộc sống hàng ngày của chúng ta. Các kiến thức toán học đã được áp dụng rộng rãi trong các lĩnh vực khác nhau, bao gồm kỹ thuật, định vị địa lý, thiết kế và xây dựng công trình, điều khiển và trong khoa học tự nhiên và xã hội học. Toán học đã giúp chúng ta hiểu được rất nhiều hiện tượng tự nhiên và cung cấp cho chúng ta các công cụ quan trọng để giải quyết các vấn đề thực tế trong cuộc sống.
Toán hình 11 bài 6 cũng có nhiều ứng dụng trong các lĩnh vực khác như:
– Trong lĩnh vực kỹ thuật: Hình học và toán học không gian được sử dụng rộng rãi để tính toán và thiết kế các thiết bị và công trình.
– Trong những bài toán định vị, Điều khiển: Các kỹ thuật định vị và định hướng sử dụng các nguyên lý của hình học và toán học không gian để chính xác định vị trí đối tượng.
– Trong thiết kế và xây dựng công trình: Hình học không gian và các công thức tính toán được sử dụng để tính toán diện tích và thể tích của các bộ phận của các công trình xây dựng, để đảm bảo chất lượng và tiết kiệm chi phí.
– Trong hệ thống định vị địa lý GPS: Các kỹ thuật định vị GPS sử dụng nguyên lý của hình học không gian để xác định vị trí của các đối tượng trên bề mặt Trái đất.
– Trong lĩnh vực khoa học tự nhiên và xã hội học: Toán học không gian được sử dụng để mô hình hóa các quá trình tự nhiên và xã hội, giúp ta hiểu rõ hơn về sự phát triển của các yếu tố này, từ đó đưa ra các giải pháp phù hợp để quản lý và phát triển chúng.
Toán hình 11 bài 6 là một chương trình học toán quan trọng cho học sinh phổ thông. Hiểu rõ các khái niệm, công thức và phương pháp giải quyết bài toán trong bài toán hình 11 bài 6 sẽ giúp học sinh áp dụng hiệu quả các kiến thức này vào thực tiễn và tạo nên những thành quả toán học đáng kể trong cuộc sống.
Từ khoá người dùng tìm kiếm: toán hình 11 bài 6 Toán hình 11 Bài 7, Toán 11 – bài 6 Đại, Bài 6 Toán Hình 11 trang 54, Khái niệm về phép dời hình và hai hình bằng nhau bài tập, Bài 7: phép vị tự, Toán 11 Phép vị tự, Toán hình 11 Bài 8, Lý thuyết Toán hình 11 Bài 6
Tag: Share 44 – toán hình 11 bài 6
Khái niệm phép dời hình và hai hình bằng nhau – Bài 6 – Toán học 11 – Thầy Lê Thành Đạt (HAY NHẤT)
Xem thêm tại đây: buoitutrung.com
Link bài viết: toán hình 11 bài 6.
Xem thêm thông tin về chủ đề toán hình 11 bài 6.
- Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- Khái Niệm Về Phép Dời Hình và Hai Hình Bằng Nhau – Toán 11
- Hình học 11 Bài 6: Khái niệm về phép dời hình và hai hình …
- Soạn hình học 11 bài 6: Khái niệm về phép dời hình và hai …
- Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- Giải Toán 11: Bài 6 trang 35 SGK Hình học 11 – Toploigiai
- Giải bài tập SGK toán 11 Chương 1-Bài 6: Khái niệm về phép …
- Bài 6 trang 114 SGK Hình học 11
Categories: https://baannapleangthai.com/img/
