TÓM TẮT
Tìm thấy 45 chủ đề phù hợp chủ đề toán hình 12 bài 3.








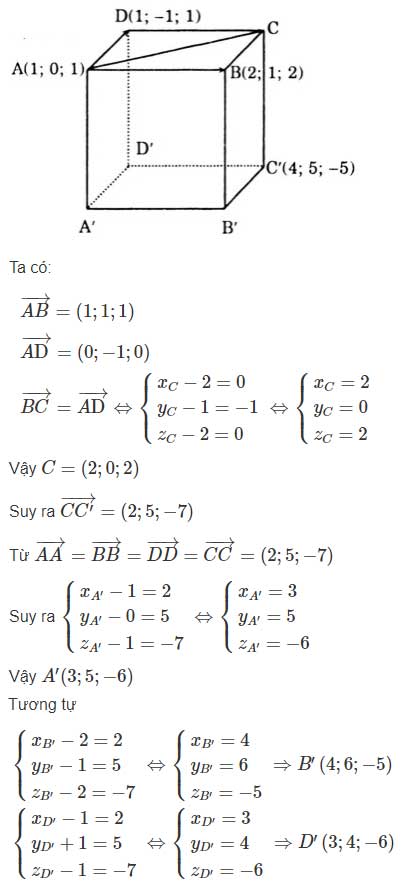
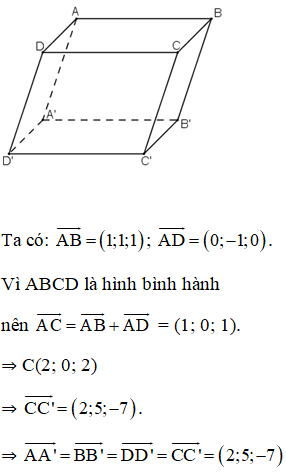





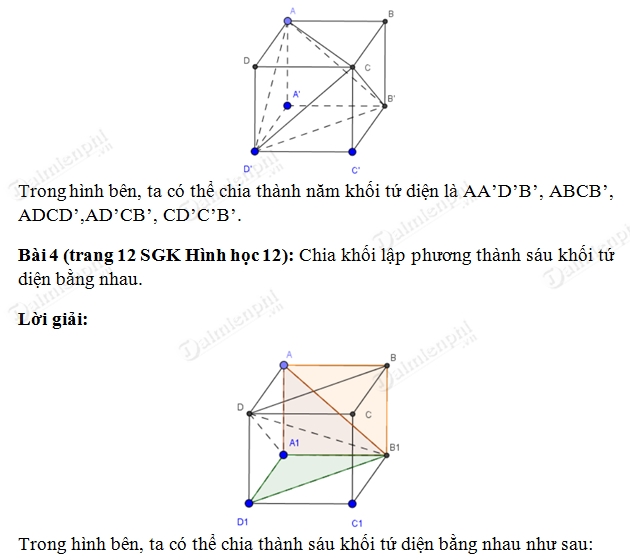





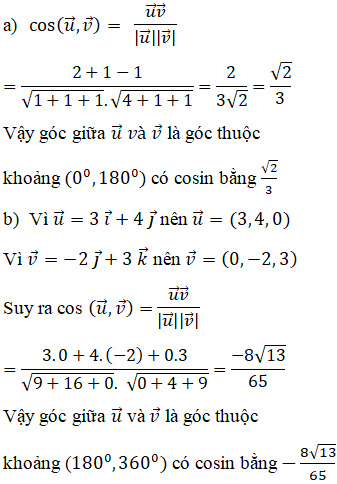


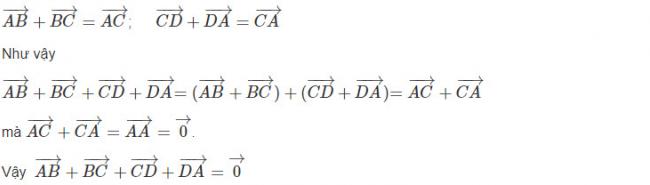









toán hình 12 bài 3
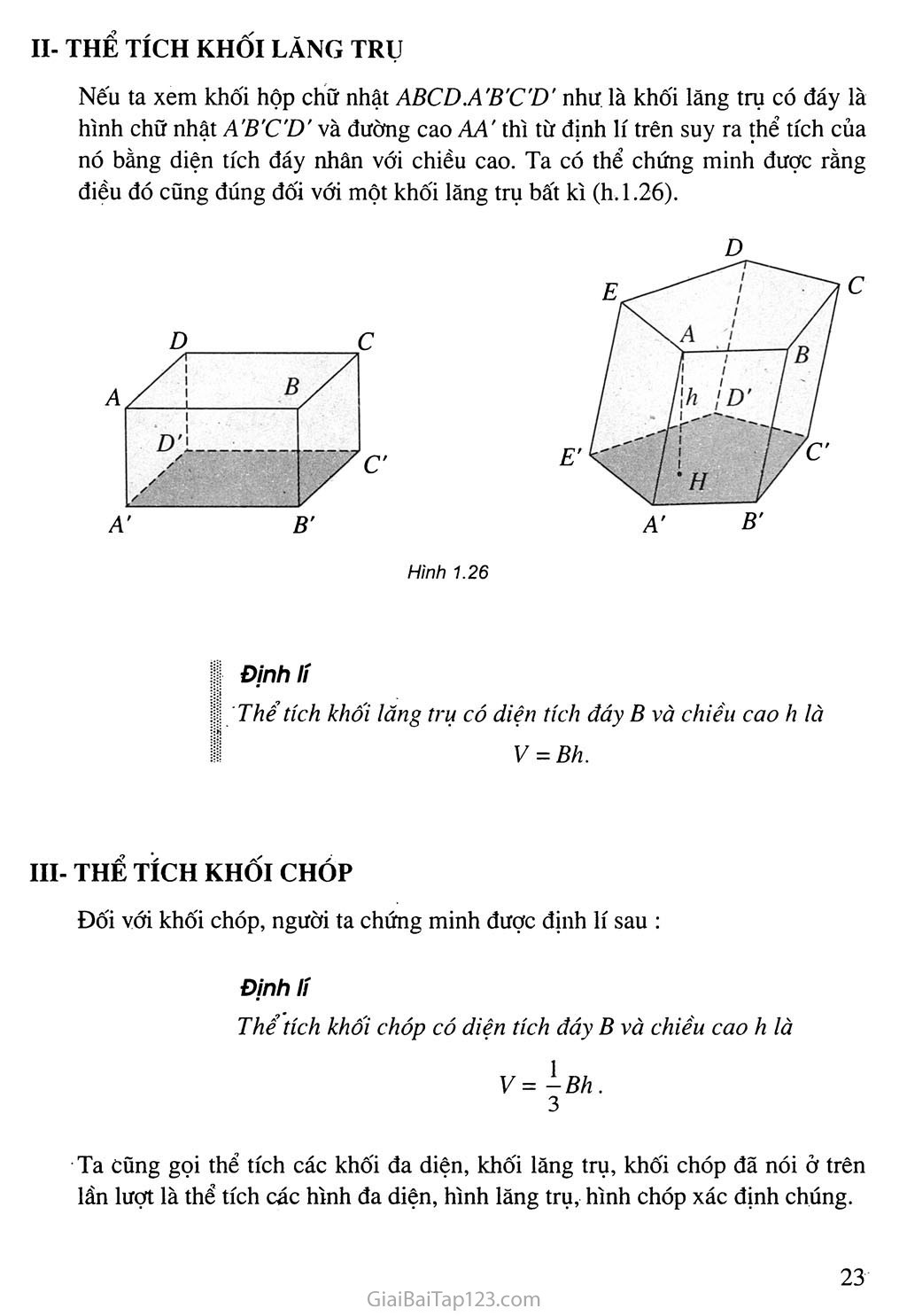
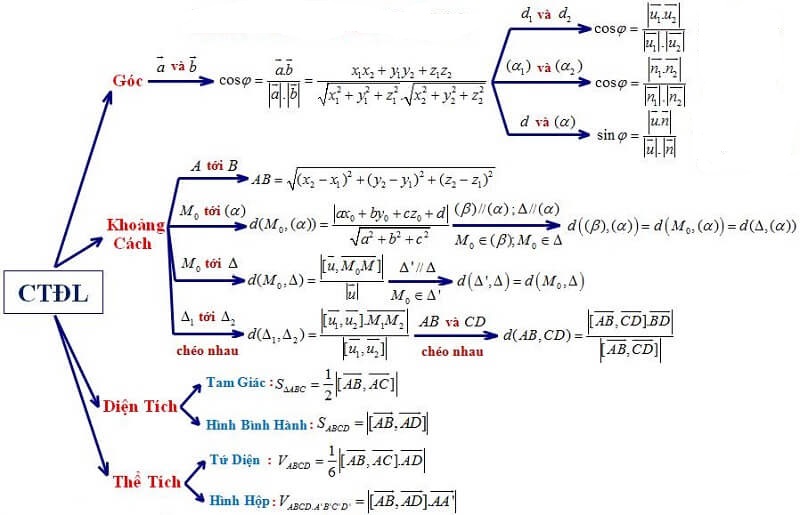
Tìm công thức tính diện tích và thể tích hình dạng đồng nhất
Để tính diện tích và thể tích hình đồng nhất, học sinh phải tìm ra công thức tính diện tích và thể tích đó. Có nhiều công thức khác nhau tùy thuộc vào loại hình đồng nhất. Ví dụ, nếu hình đồng nhất đó là hình hộp chữ nhật, công thức tính diện tích là S = 2(ab + ac + bc), và công thức tính thể tích là V = abc. Nếu hình đồng nhất đó là hình cầu, công thức tính diện tích là S = 4πr², và công thức tính thể tích là V = (4/3)πr³.
Áp dụng công thức tính diện tích và thể tích để giải các bài tập liên quan
Sau khi tìm ra công thức tính diện tích và thể tích của các hình đồng nhất, học sinh sẽ áp dụng chúng để giải các bài tập liên quan. Chẳng hạn, bài tập có thể yêu cầu tính diện tích của mặt cầu có bán kính 5 cm, hoặc tính thể tích của một khối hình chữ nhật có độ dài 10 cm, chiều rộng 5 cm, và chiều cao 8 cm.
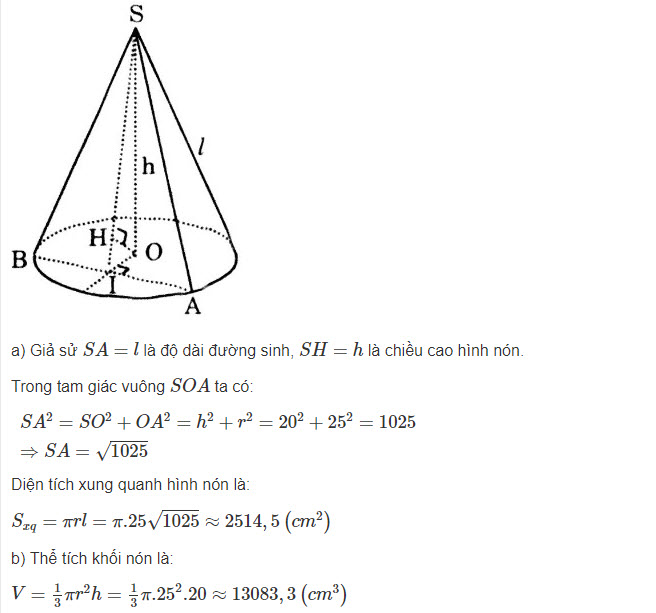
Phân tích và giải các bài tập về thể tích hình lăng trụ, hình nón, và hình cầu
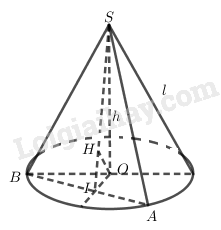
Các hình lăng trụ, hình nón, và hình cầu là các hình đặc biệt quan trọng trong toán học. Tùy thuộc vào loại hình này, học sinh phải áp dụng các công thức tính diện tích và thể tích khác nhau. Ví dụ, công thức tính diện tích của một hình lăng trụ là S = 2πrH + 2πr², và công thức tính thể tích là V = πr²H. Tương tự, nếu hình đó là hình cầu, công thức tính diện tích là S = 4πr², và công thức tính thể tích là V = (4/3)πr³.
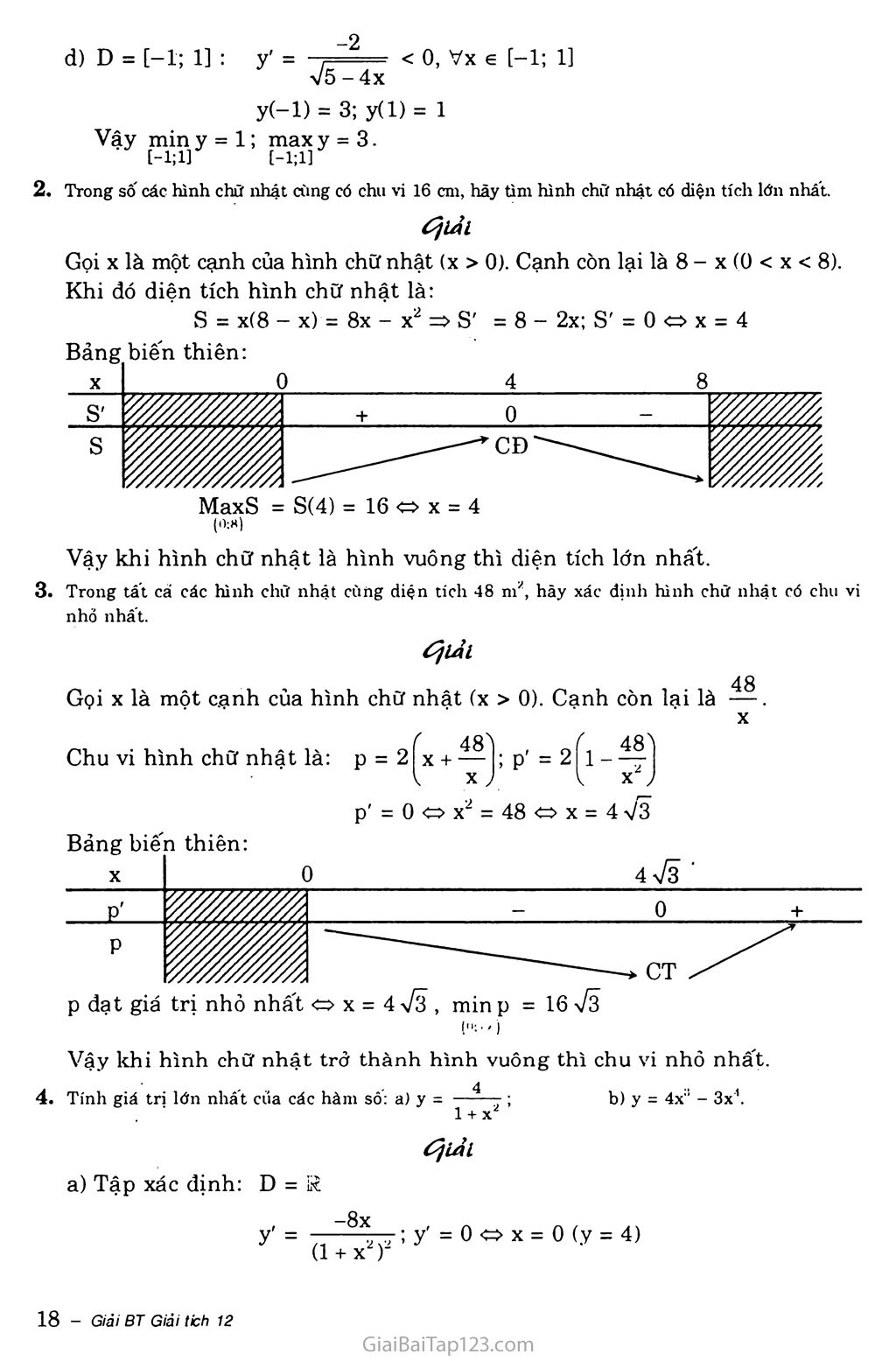
Tính toán độ dài đường chéo của hình chữ nhật và hình bình hành
Để tính toán độ dài đường chéo của một hình chữ nhật, học sinh phải sử dụng định lý Pythagoras. Đó là, nếu a và b lần lượt là chiều dài và chiều rộng của hình chữ nhật, thì đường chéo c có thể được tính bằng c = √(a² + b²). Tương tự, độ dài đường chéo của một hình bình hành cũng có thể được tính bằng cách sử dụng định lý Pythagoras.
Giải các bài tập về tính chất đối xứng của hình học và ứng dụng trong giải toán hình học
Trong toán học, học sinh phải biết rằng hình đối xứng là hình mà tồn tại trục đối xứng đối xứng qua mặt phẳng đó. Ví dụ, một hình tròn là đối xứng bởi vì bất kỳ hai điểm bên trong hình luôn có thể được nối với nhau thông qua một đoạn thằng đi qua tâm hình tròn. Học sinh cần phải biết tính chất của hình đối xứng và áp dụng chúng trong giải các bài tập liên quan.
FAQs
1. Có bao nhiêu hình đồng nhất cần phải biết trong bài tập toán hình 12 bài 3?
Có nhiều hình đồng nhất khác nhau trong bài tập toán hình 12 bài 3. Học sinh cần phải biết công thức tính diện tích và thể tích cho mỗi loại hình đó.
2. Làm thế nào để tính độ dài đường chéo của một hình bình hành?
Để tính độ dài đường chéo của một hình bình hành, bạn có thể sử dụng định lý Pythagoras.
3. Hình nào đối xứng qua tâm của nó?
Hình tròn là đối xứng qua tâm của nó.
Từ khoá người dùng tìm kiếm: toán hình 12 bài 3 toán hình 12 bài 3: phương trình đường thẳng, Toán Hình 12 Bài 3 lý thuyết, Toán Hình 12 Bài 3: phương trình đường thẳng trong không gian, Toán Hình 12 Bài 3 chương 3, Toán Hình 12 bài 3 trang 80, Bài 3 Toán Hình 12 trang 89, Toán Hình 12 bài 3 trang 39, Toán Hình 12 bài 4
Tag: Top 70 – toán hình 12 bài 3
Khái niệm về thể tích khối đa diện – Bài 3 – Toán học 12 – Thầy Trần Thế Mạnh (HAY NHẤT)
Xem thêm tại đây: buoitutrung.com
Link bài viết: toán hình 12 bài 3.
Xem thêm thông tin về chủ đề toán hình 12 bài 3.
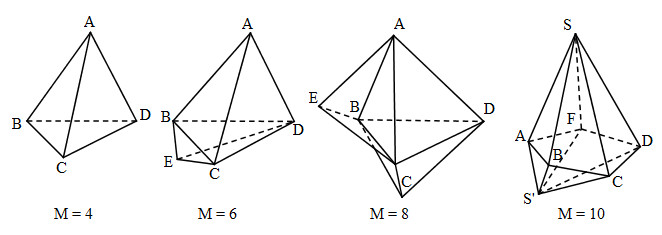
- Giải Toán 12 Bài 3: Khái niệm về thể tích của khối đa diện
- Khái niệm về thể tích của khối đa diện – Loigiaihay.com
- Giải toán 12 Bài 3. Khái niệm vê thể tích của khối đa diện
- Giải bài tập Bài 3: Khái niệm về thể tích của khối đa diện
- Hình học 12 Bài 3: Khái niệm về thể tích của khối đa diện
- Giải Toán 12: Bài 3 trang 39 SGK Hình học 12 – Toploigiai
- Bài 3: Khái niệm về thể tích của khối đa diện
- Giải bài 3 trang 39 SGK Hình học lớp 12 – soanvan.net
- Bài 3 trang 39 sách giáo khoa Hình học 12 | Giải Toán lớp 12
Categories: https://baannapleangthai.com/img/

